Prolog vs Haskell

Choose the language for your problem, not the problem for your language

I have been writing lots of notes on PROLOG and some people asked me: why PROLOG? You can solve this problems in any language! And they are right! :) I also believe that it doesn’t matter which problem you have, you can solve it in any given language.

But there is more. I also believe that it is possible to find the best language for the problem you have. No one should be too attached to any language, as every single one has ups and downs!

So I decided to add here two simple examples of PROLOG code in comparison to Haskell code - both extremely elegant IMO - and I will leave it up to you to check how it would look like in your favorite imperative language :)

Depth-First Search

The Depth-First Search is a well know algorithm, that traverses a data structure. It starts at the root and explores the branch as long as possible before backtracking.

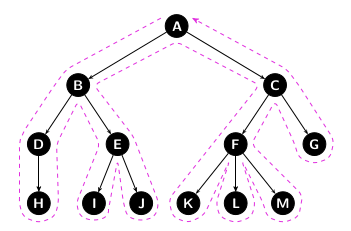
Code!

And here it goes. I am also putting them next to each other so you can compare them :)

Haskell

dfs ::(a -> Bool) -- Goaltest (goal)
  -> (a -> [a]) -- Function next (succ)
  -> [a] -- StartNode
  -> Maybe (a, [a]) -- Result: Just (GoalNode,Path)
                    -- or Nothing
  dfs goal succ stack =
    -- Add the Initial path, and then iterate
  go [(k,[k]) | k <- stack]
where
  go [] = Nothing -- Search all, nothing found
  go ((k,p):r)
    | goal k = Just (k,p) -- Goal found
    | otherwise = go ([(k’,k’:p) | k’ <- succ k] ++ r)

Prolog

result(Start,Goal):-
  path(Start,Goal,[],Path),
  write('Path: '),  % Aufruf der Tiefensuche
  write(Path).

% path(StartNode, GoalNode, List of
%         visited Node, ResultPath)

path(Node,Node,List,Path):-
  reverse(List,Path).

path(Start,Goal,List,Path):-
  edge(Start,Node),
  not(member(Node,List)),
  path(Node,Goal,[Node|List],Path).

Breadth-First Search

The Breadth-First Search is also a search algorithm, that also traverses a data structure. The difference is that it starts at the root and explores the neighbor nodes in the same level (depth) before going to the deeper level.

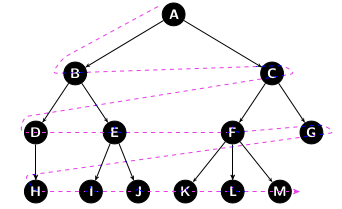
Code!

And here it goes again.

Haskell

bfs goal succ start =
go [(k,[k]) | k <- start] -- create Path
where
go [] = Nothing -- nothing found
go rs =
case filter (goal . fst) rs of -- GoalNode found?
-- No, Keep checking next
[] -> go [(k’,k’:p) | (k,p) <- rs, k’ <- succ k]
-- Yes, so stop!
(r:rs) -> Just r

Prolog

result(Start,Goal):-
         path([Start],Goal,[],Path),% Call breadth search,
         %Special: StartNodes is a list
         write('Path: '),
         write(Path).

% path(StartNodesList, GoalNodes, List der visited
                    %Nodes, ResultPath)

path(Startlist,Goal,_,Path):-
         Startlist=[Goal|_],
         reverse(Startlist,Path).

path(Startlist,Goal,List,Path):-
         Startlist=[Start|_],
         findall([Nodes|Startlist],
            (edge(Start,Nodes),
             not(member(Nodes,Startlist))),
            NodesList),
         append(List,NodesList,Listnew),
         Listnew=[PathN|RestPath],
         path(PathN,Goal,RestPath,Path).

And if you are still not sure that some languages are better for some problems, try to check the code for this problem in Java ;) Just sayin’ !