Logic & binaries

What is this post about?
Malicious codes are implemented to stay hidden during the infection and operation, preventing their removal and the analysis of the code. Software analysis is a critical point in dealing with malware, since most samples employ some sort of packing or obfuscation techniques in order to thwart analysis. It is also an area of economic concern in protecting digital assets from intellectual property theft. Static analysis tools help analysts identifying vulnerabilities and issues before they cause harm downstream. Understanding how malware works beyond standard debuggers and sandboxes gives us insights and show us how to best protect others. In this year VB conference I gave an introduction on some practical applications of SMT solvers in IT security, investigating the theoretical limitations and practical solutions, focusing on their use as a tool for binary static analysis.
This work is about :
- constraint logic programming (CLP)
- solvers
- malware RE challenges
- Logic vs. Malware
S..A..M.. What?

The satisfiability problem (SAT) asks whether the variables of a given Boolean formula (or a model) can be consistently replaced by the values 1 (or TRUE) or 0 (FALSE) in such a way that the formula evaluates to 1 (TRUE), or satisfiable. The issue here is that SAT is a NP-complete problem and like all other problems in this same complexity class, there is no efficient algorithm for solving SAT problems (that we know about!). However, SAT solvers are efficient enough for most of industrial problems and when not, we can still translate the problem into a combinatorial problem. As a result, they are frequently used as the “engine” behind various code verification applications.
Moreover, systems are usually designed and modeled at a higher level than the Boolean level and the translation to Boolean logic can be expensive. A primary goal of research in Satisfiability Modulo Theories (SMT) is to create verification engines that can reason natively at a higher level of abstraction, while still retaining the speed and automation of today’s Boolean engines.
Constraints
“Constraint programming represents one of the closest approaches computer science has yet made to the Holy Grail of programming: the user states the problem, the computer solves it.”
Eugene C. Freuder, Constraints, April 1997
Constraint Programming is nothing more than someone / something stating constraints about problem variables and finding solution which satisfies all the constraints. Of course there is a theoretical limitation when thinking about general computing problems BUT over 90% of all constraint satisfaction problems in industrial applications are finite domains problems and therefore they can be written as combinatorial problems.
Automated Theorem Proving
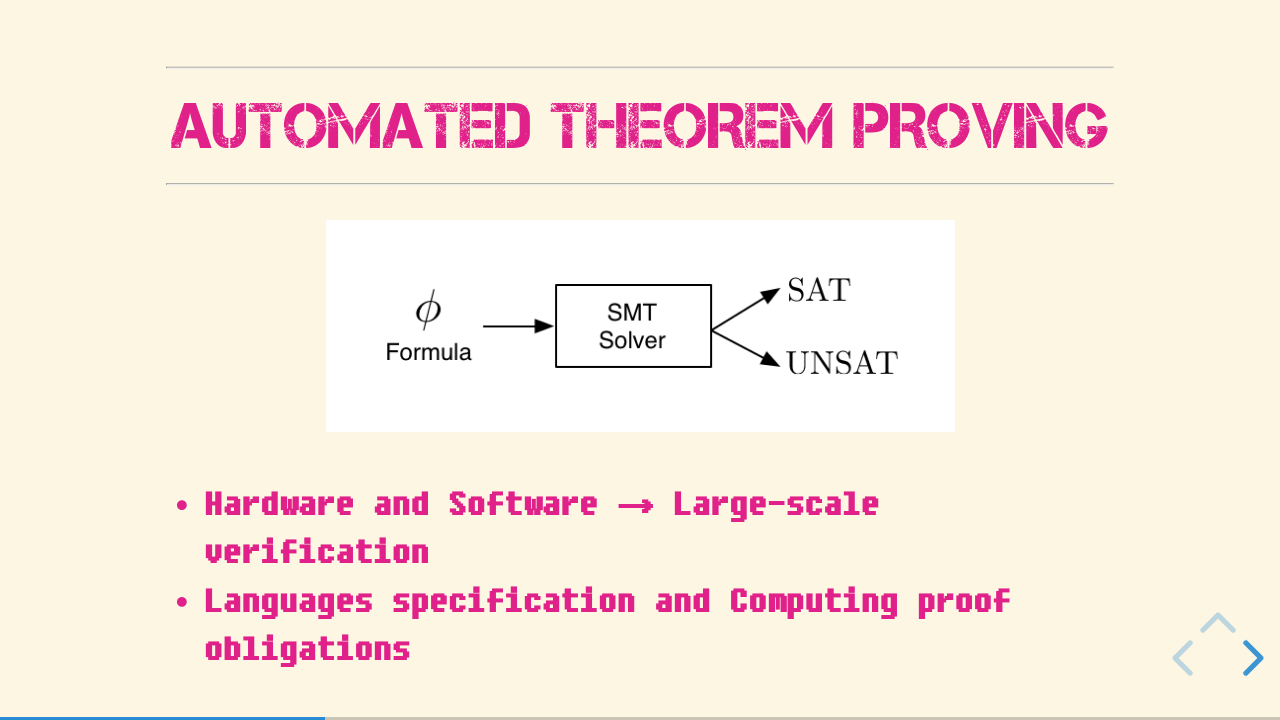
If you want to know more about logical programming, you can go around and check the other posts I have in here and I mean, this is the InternetZ, right? But for now, we can see the SMT solver as a blackbox. You feed it with a theory, which includes the problem, your start conditions and the goal you want to achieve and the “engine” inside of it will deal with the logical connections. If the engine finds a possible solution to your problem considering ALL the constrains, it will return the answer “FEASIBLE”. More than that, it will also return how to get from your problem to your desired solution! Each of this possibilities are called Instance of quantified axioms.
It is easier to understand how this blackbox works, if we know who designed it in first place. So, who wants so badly to PROVE things? In the past Mathematicians, nowadays also computer scientists working on hardware and software verification. This kind of automation was used to make the life of mathematicians a bit easier, making it possible to state (and prove) thousands of tiny theorems leading to the biggest (or highest) goal. And there is no reason for the computer scientists to not use the solvers in the same way making large-scale verification of hardware and software accessible and more reliable, defining formulas which imply the correctness of the program.
Symbolic Execution
Symbolic Execution automatically explores all program paths to determine which inputs cause each part of a program to execute. Combined with SMT Solvers which will reason about either the path is going to be takes at any given time or not, we - analysts - are able to get 100 % code coverage of the actual malware code.
It looks like that
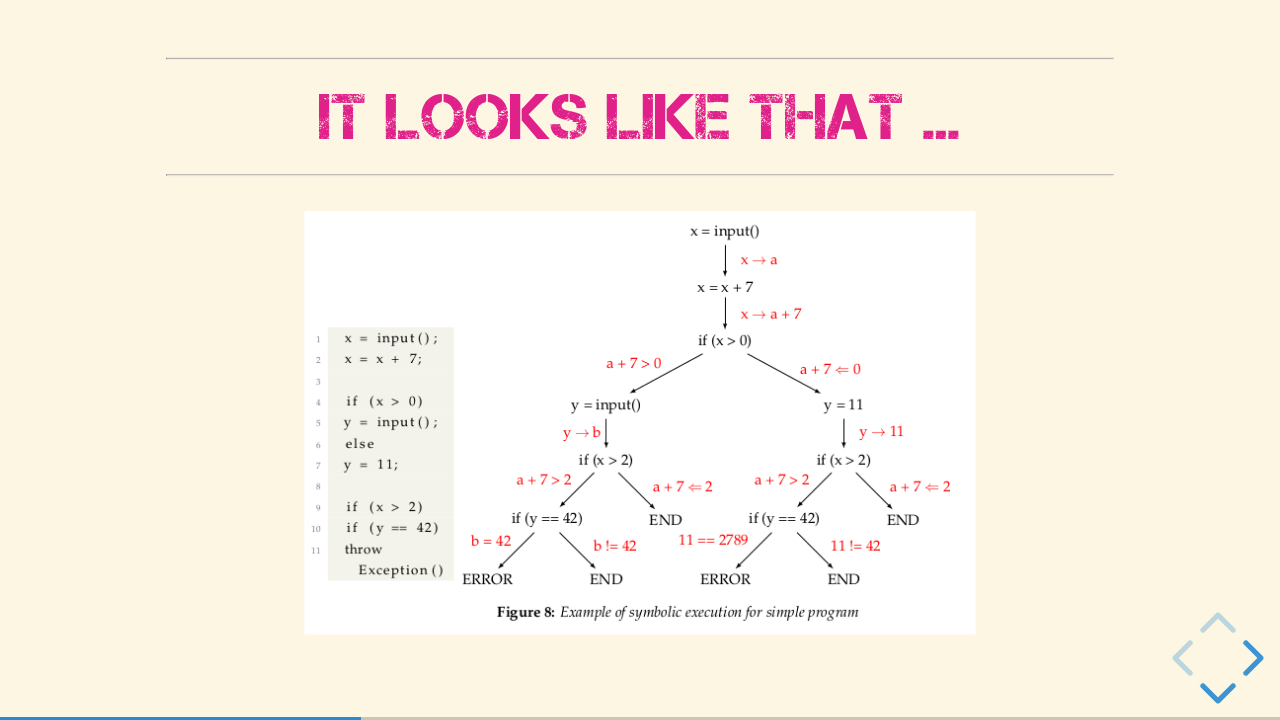
In a theoretical approach, one can say you are extending the language accepted by the Turing machine with symbolic values, which represent the unknown / possible states. Then all possible execution paths will be explored and for each path the branching constraints are collected. After that, it is possible to generate input-tests based on the collected path constraints.
How it works
A simple algorithm could be:
- Create a process (pc = 0, state = [])
- Add the process (pc, state) to the domain system D
- while D not empty:
- Remove process (pc, state) from system
- Execute it until the next branching point
- If both paths are feasible, add both to D
- if just one is feasible, add the feasible path and the negation of the not feasible path to D
It is clear to see that symbolic execution has O(e^n), where n is the number of branching points, as the Symbolic Execution Algorithm forks at every branching point, in case both paths are feasible. This is why, while implementing it, it is better to check / reason about the branch during the execution, which can limit the deep of the execution and save time and memory. When one has all the information, it is possible to create a control flow graph (CFG).
The precision of the graph and the performance of the analysis depend on the options used to generate the control flow edges. The context sensitivity of the graph is an important parameter to consider for the matter of malware detection. The configuration of the precision parameters determines the representation of system calls on the graph. High context sensitivity enables cross references, when system calls are invoked in multiple locations. The nodes can then be differentiated by the invoking function, the parameters used for the invocation or the receiving function. Context sensitivity may also depend on the functions or calls themselves. Furthermore, that means that increasing context sensitivity results in a greater number of system call clones among the graph nodes.
Keep in mind!
- Symbols as arguments
- any feasible path
- all Program states
- Symbolic values also for memory allocations
- Path conditions
Application in Security
The idea is pretty simple, as the solvers are kind of a model checking engine. One can define some safety properties naïve like X is SAFE = NOTHING BAD EVER happens. This way, one can infer that the model M is a transition. To check, if M is safe in P (P being a state property), it computes all reachable states R and then calculate the intersection between R and P, which should be the empty set (not existent). We could also represent M symbolically and use other automata-based methods. People are using SMT solvers in different fields, these are only some examples:
Bug Hunting

- Fuzzing
- Code verification
- Binary Analysis
Exploitation
- Proof of Concept
- AEG
- APG
Malware analysis

- Obfuscation
- Compiler optimizations
- Crypto-analysis
Binary Obfuscation
One thing that made me fall in love with malware is its duality. Malware is technically and educationally really interesting and some techniques are not really different than things used for example on software protection systems. In both cases, there is a program that does something and somebody puts some stuff around that program to make it difficult to people that are not allowed to get access to this program to actually understand what is going on.

In one case, the objective is to make the analysis of the program difficult so that malware analysts have a tough time figuring out what the malicious code does and of course how to stop or neutralized those actions. In the other case, the objective is to make the analysis of the program difficult so crackers have a tough time figuring out what the key check program does and how to neutralize those protections. An important thing about this is that malware development is illegal but software protection is perfectly legal. What lead us to the main difference that is what the protected program actually does. There is nothing wrong with a program that does disk management for you, but it is very bad if, instead of that, the program encrypts all the files in the computer and ask for ransom.
Malware Deobfuscation

The implementation of obfuscation can be as simple as a few bit manipulations - like binary Xor - and as advanced as cryptographic standards (i.e. DES, AES, etc). In the world of malware, it’s useful to hide significant words the program uses (called “strings”) because they give insight into the malware’s behavior. Examples of said strings to hide would be malicious URLs or registry keys.
Obfuscation techniques

An easy way to obfuscate code or make the binary code looks complex is the implementation of “while” or “go to” checks that are always true for example, creating an amount of called “garbage code”. Such code is mostly generated by the compiler, if you just give the command “No Optimization”. Using SMT solvers, it is possible to check each of the basic blocks, looking for ways of simplify the code if the constraint match. With aid of symbolic execution we can also check for unused branching points or unreachable code. Another exclusive or operation (represented as XOR) is probably the most commonly used method of obfuscation. This is because it is very easy to implement and easily hides your data from untrained eyes. Using SMT solvers and logical programming, it is possible to easily create a tool that will check for possible keys of the XOR function. Each possible key will be one instance of the SMT solver solution set. The XOR function is our theory and the SMT solver will check if it is feasible to get readable strings, for example, from the bytes that we have. But remember:

For packers’ sake

And sometimes malware writers go a step further and obfuscate the entire file with a special program called a packer. Using SMT solvers it is also possible to unpack the code without needing to actually run it, avoiding the cases where the actually malicious code is inside the self implemented packer. This is possible because the SMT solver will give us instances of possible unpacked code. (Yes, I am saying static generic unpacking - fancy right?)
Implementation

There is a control flow implementation of all the conditional jump instructions which takes the 2 operands to compare, the conditional operand and the location operand. The SMT solver will reason about the conditional operand against the two comparison operands and if the condition is met, it will set the EIP to the value of the location operand. Otherwise it will go to the next instruction. If one of the condition is impossible to meet (the false or the true), the solver will remove the whole path starting from that branching point.
Limitations
Theoretical

The Rice’s theorem postulates that whatever properties of programs we are interest in, no other program can tell us, if this property holds for every program. We can reduce the Rice’s theorem to the Halting problem. The Halting problem postulates, that we cannot know if the computation of a program on some input will ever terminate. The importance of the undecidability of the Halting problem lies in its generality. A device that is capable of computing the solution to any problem that can be computed, provided that the device is given enough storage and time for the computation to finish, is defined as universal computing machine - also known as Turing machine. Turing also conjectured that his definition of computable was identical to the ’natural’ definition evinces that if a problem cannot be solved by a Turing machine also it cannot be solved in any other systematic manner.
Practical
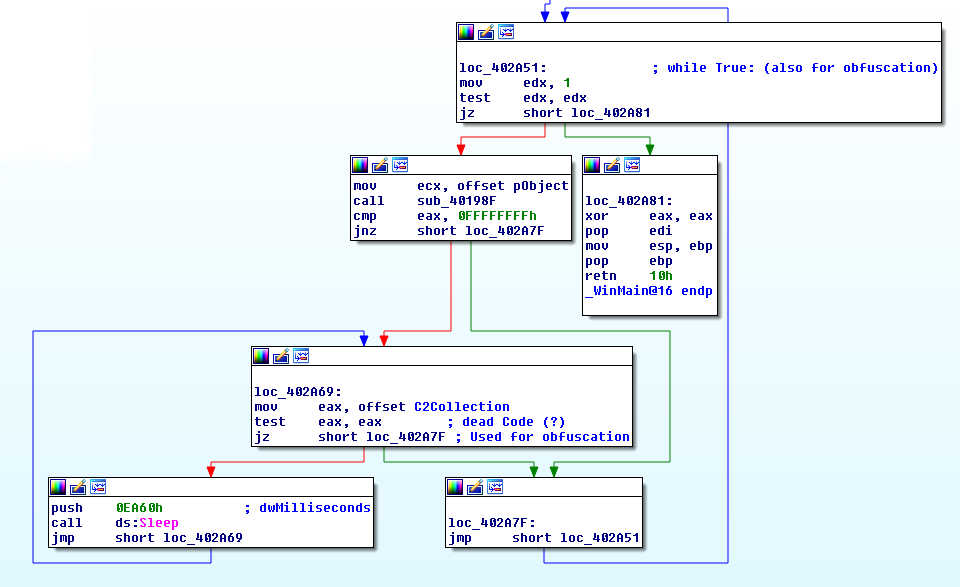
The precision of the graph and the performance of the analysis depend on the options used to generate the control flow edges. The context sensitivity of the graph is an important parameter to consider for the matter of malware detection. The configuration of the precision parameters determines the representation of system calls on the graph. High context sensitivity enables cross references, when system calls are invoked in multiple locations. The nodes can then be differentiated by the invoking function, the parameters used for the invocation or the receiving function. Context sensitivity may also depend on the functions or calls themselves. Furthermore, that means that increasing context sensitivity results in a greater number of system call clones among the graph nodes. Accordingly, it also directly increases the analysis precision. However, the graph construction may become exponentially resource expensive for the processor.
In most of the cases, static analysis is a balance between wanted or needed precision and availability of resources. This process is repeated for all paths acquired. Afterwards, a set of satisfiable formulas is generated. Each of the satisfiable formulas in this set represents a trigger condition of a new discovered path. Each of these paths depends on the system calls. Hence, the solver is able to build the trigger values - that means, the used system calls - and the values for the trigger inputs, which are necessary to observe the malicious code.
Conclusion
Learnings / Take away

- Symbolic execution is a powerful tool while analysing malware
- SMT solvers can be used to simplify CFG and support analysts while reversing
SMT solvers are becoming an integral part of security engineer’s tool kit. I hope more people can see why solvers do a remarkable job in assisting malware analysts. The support in deciding whether suggested solutions are valid in their respective problem space saves economical resources and time of experts. Solvers support analysts looking for code vulnerabilities and analysing malicious code, detecting vulnerabilities in web applications and breaking encryptions. Yet, solvers are not suited for generating domain-specific problem descriptions. The preliminary constraint generation step still has to be performed outside the solver.
Work done:

- a binary garbage-code eliminator for malware analysis,
- a XOR search,
- some cryptographic algorithm breaker,
- a generic unpacker,
- a binary structure recognizer,
- a C++ class hierarchy reconstructor.
Working on …

- r2 integration,
- maybe IDA-Plugin.
On other matters I am also working on building a specialized constraint inference assistant, which will improve and help the generation of formal problem definitions for non-trivial problems in the area of computer security. And it is good to remember that improving the constraint generation phase making will make automated exploit generation finally practicable. Of course, improving SMT solvers in general would also mean a progress towards serial check and more secure cryptosystems.
If you like this topic, you can find more information on my VB paper!
You can also find the full slide deck here.
this has been written by me for fun purposes, don't take it serious!